A.
Teorema Pythagoras
Pythagoras menyatakan bahwa : “Untuk setiap segitiga
siku-siku berlaku kuadrat panjang sisi miring (Hipotenusa) sama dengan jumlah
kuadrat panjang sisi siku-sikunya.”
jika c adalah panjang sisi miring/hipotenusa
segitiga, a dan b adalah panjang sisi siku-siku. Berdasarkan teorema Pythagoras
di atas maka diperoleh hubungan:
c2 = a2 + b2
Dalil pythagoras di atas dapat diturunkan menjadi:
a2 = c2 – b2
b2 = c2 – a2
Catatan : Dalam menentukan persamaan Pythagoras yang perlu
diperhatikan adalah siapa yang berkedudukan sebagai hipotenusa/sisi miring.
Contoh :
Tentukan rumus pythagoras dan turunan dari segitiga yang memiliki
panjang sisi miring a dan sisi siku-sikunya b dan c.
Rumus Pythagoras : a2 = b2 + c2
Turunannya
: b2 = a2 – c2
c2
= a2 – b2
B. Menghitung Panjang sisi segitiga siku-siku
Contoh :
1. Pada suatu segitiga ABC siku-siku di titik A. panjang AB= 4 cm
dan AC= 3 cm. Hitunglah panjang BC!
Jawab:
BC2 = AC2 + AB2
BC2 = 32 + 42
BC2 = 9 + 16
BC2 = 25
BC = 5 cm
2. Panjang sisi siku-siku dalam segitiga siku-siku adalah 4x cm
dan 3x cm. Jika panjang sisi hipotenusanya 20 cm. Tentukan nilai x.
AC2 = AB2 + BC2
202 = (4x)2 + (3x)2
400 = 16x2 + 9x2\
400 = 25x2
16 = x2
= x
3. Sebuah kapal berlayar ke arah Barat sejauh 80 km, kemudian ke
arah utara sejauh 60 km. Hitunglah jarak kapal sekarang dari jarak semula.
jawab:
OU2 = OB2 + UB2
OU2 = 802 + 602
OU2 = 6.400 + 3.600
OU2 = 10.000
OU = 100 km
C. Menentukan Jenis Segitiga jika Diketahui Panjang Sisinya dan Triple Pythagoras
1. Kebalikan Dalil Pythagoras
Dalil pythagoras menyatakan bahwa dalam segitiga ABC, jika sudut A
siku-siku maka berlaku a2= b2 + c2.
Dalam ABC, apabila a adalah sisi dihadapan sudut A, b
adalah sisi dihadapan sudut B, c adalah sisi sihadapan sudut C, maka berlaku
kebalikan Teorama Pythagoras, yaitu:
Jika a2 = b2 + c2 maka ABC siku-siku di A.
Jika b2 = a2 +c2 maka ABC siku-siku di B.
Jika c2 = a2 + b2 maka ABC siku-siku di C.
Dengan menggunakan prinsip kebalikan dalil Pythagoras, kita dapat
menentukan apakah suatu segitiga merupakan segitiga lancip atau tumpul.
Jika a2 = b2 + c2 maka ABC adalah segitiga
siku-siku.
Jika a2 > b2 + c2 maka ABC adalah segitiga
tumpul.
Jika a2 < b2 + c2 maka ABC adalah segitiga
lancip.
Contoh :
Tentukan jenis segitiga yang memiliki panjang sisi
1. 5 cm, 7 cm dan 8 cm.
Jawab: sisi terpanjang adalah 8 cm, maka a= 8 cm, b = 7cm dan c =
5 cm
a2 = 82 = 64
b2 + c2 = 72 + 52
b2 + c2 = 49 + 25
b2 + c2 = 74
karena a2 < b2 + c2, maka segitiga tersebut adalah segitiga
lanci
2. 8cm, 7cm dan 12 cm
Jawab: sisi terpanjang adalah 12 cm, maka a= 12 cm, b = 7cm dan c
= 8 cm
a2 = 122 = 144
b2 + c2 = 72 + 82
b2 + c2 = 49 + 64
b2 + c2 = 113
karena a2 > b2 + c2, maka segitiga tersebut adalah segitiga
tumpul
2. Triple Pythagoras
Yaitu pasangan tiga bilangan bulat positif yang memenuhi kesamaan
“kuadrat bilangan terbesar sama dengan jumlah kuadrat kedua bilangan yang
lain.”
Contoh :
3, 4 dan 5 adalah triple Pythagoras sebab, 52 = 42 + 32
CONTOH SOAL :
1 . Diberikan sebuah segitiga siku-siku pada gambar berikut
ini:
Tentukan panjang sisi miring segitiga!
2 . Diberikan sebuah segitiga siku-siku pada gambar berikut ini:
Tentukan panjang sisi alas segitiga!
3 . Sebuah segitiga siku-siku memiliki sisi miring sepanjang 35 cm dan sisi alas memiliki panjang 28 cm.
Tentukan luas segitiga tersebut!
4 . Perhatikan gambar segitiga berikut!
Tentukan panjang sisi AB!
5 . Perhatikan gambar segitiga ABC berikut ini!
Jika panjang AC 12√3 cm dan sudut C sebesar 30°, tentukan panjang AB dan panjang BC!
JAWABAN :
1. Pembahasan
AB = 6 cm
BC = 8 cm
AC = ......
Mencari sisi miring sebuah segitiga dengan teorema pythagoras:
2 . Pembahasan
PR = 26 cm
PQ = 10 cm
QR = ......
Menentukan salah satu sisi segitiga yang bukan sisi miring:
3 . Pembahasan
Tentukan tinggi segitiga terlebih dahulu:
Luas segitiga adalah setengah alas dikali tinggi sehingga didapat hasil:
4 . Pembahasan
Perbandingan panjang sisi-sisi pada segitiga siku-siku dengan
sudut 45° adalah sebagai berikut:
Bandingkan sisi-sisi yang bersesuaian didapat:
Berikutnya akan dibahas soal-soal segitiga yang menggunakan
perbandingan dengan sudut-sudut 30o dan 60o
5 . Pembahasan
Tengok perbandingan sisi-sisi pada segitiga siku-siku yang
mengandung sudut 30° dan 60° kemudian kita buat perbandingan dengan segitiga
ABC:
Dari sisi-sisi yang bersesuaian diperoleh:







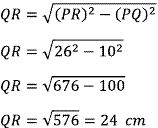






0 comments:
Post a Comment